Selasa, 01 April 2014

SPK Menggunakan Metode AHP

Analytical Hierarchy Process (AHP) dikembangkan oleh Thomas L. Saaty pada tahun 1970-an. Metode ini merupakan salah satu model pengambilan keputusan multikriteria yang dapat membantu kerangka berpikir manusia dimana faktor logika, pengalaman pengetahuan, emosi dan rasa dioptimasikan ke dalam suatu proses sistematis. Pada dasarnya, AHP merupakan metode yang digunakan untuk memecahkan masalah yang kompleks dan tidak terstruktur ke dalam kelompok –kelompoknya, dengan mengatur kelompok tersebut ke dalam suatu hierarki, kemudian emasukkan nilai numerik sebagai pengganti persepsi manusia dalam melakukan perbandingan relatif. Dengan suatu sintesa maka akan dapat ditentukan elemen mana yang mempunyai prioritas tertinggi.
AHP merupakan suatu pendekatan praktis untuk memecahkan masalah keputusan kompleks yang meliputi perbandinagn alternatif. AHP juga memungkinkan pengambilankeputusan menyajikan hubungan hierarki antara faktor, atribut, karakteristik atau alternative dalam lingkungan pengambilan keputusan. Dengan cirri – ciri khusus, hierarki yang dimilikinya, masalah kompleks yang tidak terstruktur dipecahkan dalam kelompok -kelompoknya.
Skala ukuran panjang (meter), temperature (derajat), waktu (detik) dan uang (rupiah) telah digunakan dalam kehidupan sehari-hari untuk mengukur bermacam-macam kejadian yang sifatnya fisik. Kita tahu bahwa penerapan seperti itu dapat diterima secara umum. Pertanyaannya adalah apakah kita dapat memperluas dan membenarkan penggunaan skala tersebut secara beralasan dan mudah dipahami untuk mencerminkan perasaan-perasaan kita pada bermacam-macam persoalan sosial, ekonomi dan politik?
Sulit dibayangkan, sebab di sini lebih cocok bila digunakan suatu ukuran lain yang lebih sederhana, misalnya persentase. Namun variabel-variabel sosial, ekonomi, dan politik tidak jarang yang sulit diukur, seperti misalnya bagaimana mengukur produk yang berupa rasa aman karena tidak adanya serangan dari Negara lain yang dihasilkan karena pengeluaran pemerintah di bidang pertahanan, bagaimana mengukur kerugian yang diderita masyarakat karena bermacam-macam polusi dan kerusakan lingkungan akibat industrialisasi, dan sebagainya.
Oleh karena itu, maka diperlukan suatu skala yang luwes yang disebut prioritas, yaitu suatu ukuran abstrak yang berlaku untuk semua skala. Penentuan prioritas inilah yang akan dilakukan dengan menggunakan AHP. Dalam menyelesaikan persoalan dengan AHP ada beberapa prinsip yang harus dipahami :
Dekomposisi
Setelah persoalan didefenisikan, maka perlu dilakukan decomposition yaitu memecah persoalan yang utuh menjadi unsur – unsurnya. Jika ingin mendapatkan hasil yang akurat, pemecahan juga dilakukan terhadap unsur – unsurnya sampai tidak mungkin dilakukan pemecahan lebih lanjut, sehingga didapatkan beberapa tingkatan dari persoalan tadi. Karena alasan ini, maka proses analisis ini dinamakan hierarki (hierarchy). Ada 2 (dua) jenis hierarki, yaitu lengkap dan tak lengkap. Dalam hierarki lengkap, semua elemen pada suatu tingkat memiliki semua elemen yang ada pada tingkat berikutnya. Jika tidak demikian dinamakan hierarki tak lengkap.
Penilaian Berpasangan
Prinsip ini berarti membuat penilaian tentang kepentingan relatif 2 (dua) elemen pada suatu tingkat tertentu dalam kaitannya dengan tingkat di atasnya. Penilaian ini merupakan inti dari AHP, karena ia akan berpengaruh terhadap prioritas elemen – elemen. Hasil dari penilaian ini akan tampak lebih enak bila disajikan dalam bentuk matriks yang dinamakan matriks Pairwise Comparison.(Penilaian Berpasangan).
Agar diperoleh skala yang bermanfaat ketika membandingkan 2 (dua) elemen, seseorang yang akan memberikan jawaban perlu pengertian menyeluruh tentang elemen – elemen yang dibandingkan dan relevansinya terhadap kriteria atau tujuan yang dipelajari. Dalam penyusunan skala kepentingan ini, digunakan patokan tabel :
Skala Dasar Thomas L. Saaty

Langkah dan Prosedur AHP
Buchara (2000) mejelaskan bahwa secara umum, langkah – langkah yang harus dilakukan dalam menggunakan AHP untuk memecahkan suatu masalah adalah sebagai berikut :
1. Mendefenisikan permasalahan dan menentukan tujuan. Bila AHP digunakan untuk memilih alternatif atau menyusun prioritas alternatif, maka tahap ini dilakukan pengembangan alternatif.
2. Menyusun masalah ke dalam suatu struktur hierarki sehingga permasalahan yang kompleks dapat ditinjau dari sisi yang detail dan terukur
3. Menyusun prioritas untuk tiap elemen masalah pada setiap hierarki. Prioritas ini dihasilkan dari suatu matriks perbandingan berpasangan antara seluruh elemen pada tingkat hierarki yang sama.
4. Melakukan pengujian konsistensi terhadap perbandingan antar elemen yang didapatkan pada tiap tingkat hierarki.

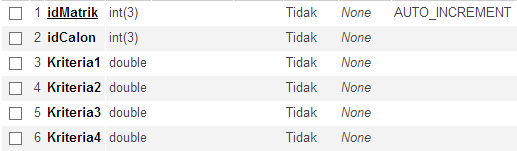
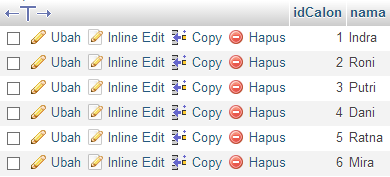
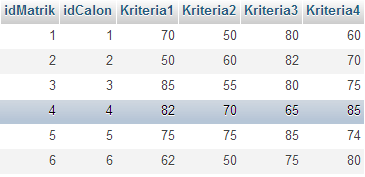
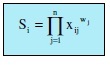
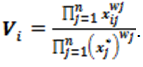SPK Menggunakan Metode Profile Matching (GAP)

Profile matching merupakan suatu proses yang sangat penting dalam manajemen SDM dimana terlebih dahulu ditentukan kompetensi (kemampuan) yang diperlukan oleh suatu jabatan. Kompetensi/kemampuan tersebut haruslah dapat dipenuhi oleh pemegang/calon pemegang jabatan.

Dalam proses profile matching secara garis besar merupakan proses membandingkan antara kompetensi individu kedalam kompetensi jabatan sehingga dapat diketahui perbedaan kompetensinya (disebut juga gap), semakin kecil gap yang dihasilkan maka bobot nilainya semakin besar yang berarti memiliki peluang lebih besar untuk karyawan menempati posisi tersebut.

Untuk menganalisis karyawan yang sesuai dengan jabatan tertentu dilakukan dengan metode profile matching, dimana dalam proses ini terlebih dahulu menentukan kompetensi (kemampuan) yang diperlukan oleh suatu jabatan. Dalam proses profile matching secara garis besar merupakan proses membandingkan antara kompetensi individu ke dalam kompetensi jabatan sehingga dapat diketahui perbedaan kompetensinya (disebut juga gap)

1. Perhitungan Pemetaan GAP Kompetensi
Setelah proses pemilihan kandidat, proses berikutnya adalah menentukan kandidat mana yang paling cocok menduduki jabatan yang diajukan oleh perusahaan. Dalam kasus ini penulis menggunakan perhitungan pemetaan gap kompetensi dimana yang dimaksud dengan gap disini adalah beda antara profil jabatan dengan profil karyawan atau dapat ditunjukkan pada rumus di bawah ini:

Gap = Profil Karyawan – Profile Jabatan

2. Perhitungan Pemetaan GAP Kompetensi Berdasarkan Aspek-Aspek
Untuk perhitungan pemilihan karyawan pengumpulan gap-gap yang terjadi itu sendiri pada tiap aspeknya mempunyai perhitungan yang berbeda-beda. Untuk keterangannya bisa dilihat pada tabel 2.1 :

Tabel 3.2 Keterangan Sub Aspek Kriteria

Kriteria	Keterangan Sub Kriteria
Aspek Kapasitas Intelektual	CS : Common Sense
	VI : Verbalisasi Ide
	SB : Sistematika Berfikir
	PSR : Penalaran dan Solusi Real
	KN : Konsentrasi
	LP : Logika Praktis
	FB : Fleksibilitas Berfikir
	IK : Imajinasi Kreatif
	ANT : Antisipasi
	IQ : Potensi Kecerdasan
Aspek Sikap Kerja	EP : Energi Psikis
	KTJ : Ketelitian dan Tanggung Jawab
	KH : Kehati-hatian
	PP : Pengendalian Perasaan
	DB : Dorongan Berprestasi
	VP : Vitalitas dan Perencana
Aspek Perilaku	D : Dominance (Kekuasaan)
	I : Influences (Pengaruh)
	S : Steadiness (Keteguhan Hati)
	C : Compliance (Pemenuhan)

Di mana nilai aspek sub kriterianya adalah sebagai berikut :

Tabel 3.3 Nilai aspek sub kriteria

Nilai Sub Kreteria	1 : Tidak Memenui Syarat
	2 : Kurang
	3 : Cukup
	4 : Baik
	5 : Sangat Baik

1. Perhitungan dan Pengelompokan Core dan Secondary FactorSetelah menentukan bobot nilai gap untuk ketiga aspek yaitu aspek kapasitas intelektual, sikap kerja dan perilaku dengan cara yang sama. Kemudian tiap aspek dikelompokkan menjadi 2 (dua) kelompok yaitu kelompok Core Factor dan Secondary Factor. Untuk perhitungan core factor dapat ditunjukkan pada rumus di bawah ini:

NCF = Σ NC (I, s, p)

Σ IC

Keterangan:

NCF : Nilai rata-rata core factor

NC(i, s, p) : Jumlah total nilai core factor (Intelektual, Sikap kerja, Perilaku)

IC : Jumlah item core factor

Sedangkan untuk perhitungan secondary factor dapat ditunjukkan pada rumus di bawah ini:

NCS = Σ NS (I, s, p)

Σ IS

Keterangan:

NSF : Nilai rata-rata secondary factor

NS(i, s, p) : Jumlah total nilai secondary factor (Intelektual, Sikap kerja, Perilaku)

IS : Jumlah item secondary factor

Minggu, 30 Maret 2014

SPK Menggunakan PHP

Penerapan Metode Sistem Pendukung Keputusan SAW

Metode sistem pendukung keputusan SAW (Simple additive Weighting) merupakan salah satu metode Sistem Pendukung Keputusan yang menggunakan konsep penjumlahan terbobot.

Penerapan Metode Sistem Pendukung Keputusan SAW dengan PHP
Proses dari metode Simple additive weighting :

Siapkan terlebih dahulu data yang disimpan dalam Matrik Data.
Lakukan Normalisasi Matrik Data dengan formula :

Normalisasi Matrik SAW
Lakukan perangkingan dengan Formula

1

Vi = (rij * wi) + (rij * wi) + .. (rxx * wx)

Sebagai bahan Penerapan Metode SAW, berikut contoh kasus yang melakukan perhitungan dengan PHP.

Suatu Institusi Perguruan tinggi akan memilih seorang karyawan untuk dipromosikan sebagai kepala unit Sistem Informasi.
Ada empat kriteria yang digunakan untuk melakukan penilaian yaitu :

C1 = Tes Pengetahuan (Wawasan) Sistem Informasi.

C2 = Praktik Insatalasi Jaringan

C3 = Tes Kepripadian

C4 = Tes Pengetahuan Agama.

Pengambil keputusan memberikan bobot untuk setiap kriteria sebagai berikut: C1 = 35%; C2 = 25%; C3 = 25%; dan C4 = 15%.

Ada enam orang karyawan yang menjadi kandidat (alternatif) untuk dipromosikan sebagai kepala unit, yaitu:

A1 = Indra

A2 = Roni,

A3 = Putri,

A4 = Dani,

A5 = Ratna, dan

A6 = Mira.

Data diatas sekarang kita rubah ke dalam database, buat database kira2 seperti ini :
tbcalon :

Tabel Calon Sistem Pendukung Keputusan

Selanjutnya kita buat tabel untuk menyimpan matrik, misal tbmatrik :

Tabel Matrik Sistem Pendukung Keputusan

Setelah keduanya dibuat, silahkan isi data sehingga terbentuk data seperti ini :
tbcalon :

Data Calon SPK

dan data Matrik :

Data Matrik Calon SPK

Langkah-langkah perhitungan sistem pendukung keputusan dengan php :

Lakukan Langkah ke 2, yakni normalisasi :

//Lakukan Normalisasi dengan rumus pada langkah 2

    //Cari Max atau min dari tiap kolom Matrik

    $crMax = mysql_query("SELECT max(Kriteria1) as maxK1, 

                        max(Kriteria2) as maxK2,

                        max(Kriteria3) as maxK3,

                        max(Kriteria4) as maxK4 

            FROM tbmatrik");

    $max = mysql_fetch_array($crMax);

    //Hitung Normalisasi tiap Elemen

    $sql2 = mysql_query("SELECT * FROM tbmatrik");

    //Buat tabel untuk menampilkan hasil

    echo "<H3>Matrik Normalisasi</H3>

    <table width=500 style='border:1px; #ddd; solid; border-collapse:collapse' border=1>

        <tr>

            <td>No</td><td>Nama</td><td>C1</td><td>C2</td><td>C3</td><td>C4</td>

        </tr>

        ";

    $no = 1;

    while ($dt2 = mysql_fetch_array($sql2)) {

        echo "<tr>

            <td>$no</td><td>".getNama($dt2['idCalon'])."</td><td>".round($dt2['Kriteria1']/$max['maxK1'],2)."</td><td>".round($dt2['Kriteria2']/$max['maxK2'],2)."</td><td>".round($dt2['Kriteria3']/$max['maxK3'],2)."</td><td>".round($dt2['Kriteria4']/$max['maxK4'],2)."</td>

        </tr>";

    $no++;

    }

    echo "</table>";

Selanjutnya lakukan Perangkingan :

//Proses perangkingan dengan rumus langkah 3

    $sql3 = mysql_query("SELECT * FROM tbmatrik");

    //Buat tabel untuk menampilkan hasil

    echo "<H3>Perangkingan</H3>

    <table width=500 style='border:1px; #ddd; solid; border-collapse:collapse' border=1>

        <tr>

            <td>No</td><td>Nama</td><td>Rangking</td>

        </tr>

        ";

    $no = 1;

    //Kita gunakan rumus (Normalisasi x bobot)

    while ($dt3 = mysql_fetch_array($sql3)) {

        echo "<tr>

            <td>$no</td><td>".getNama($dt3['idCalon'])."</td>

            <td>"

            .round((($dt3['Kriteria1']/$max['maxK1'])*$bobot[0])+

            (($dt3['Kriteria2']/$max['maxK2'])*$bobot[1])+

            (($dt3['Kriteria3']/$max['maxK3'])*$bobot[2])+

            (($dt3['Kriteria4']/$max['maxK4'])*$bobot[3]),2)."</td>

        </tr>";

    $no++;

    }

    echo "</table>";

Selesai, berikut adalah perhitungan sistem pendukung keputusan dengan PHP :

Hasil Sistem Pendukung Keputusan

SPK Menggunakan Metode WP

Metode WP (Weigted Product) merupakan salah satu metode sistem pendukung keputusan, dimana perkalian digunakan untuk menghubungkan rating atribut, dan rating setiap atribut harus dipangkatkan dulu dengan bobot atribut yang bersangkutan. Untuk Lebih jelasnya berikut ini adalah algoritma metode weighted product :

Persiapkan terlebih dahulu bobot dan lakukan perbaikan bobot dengan :
W _j= W_j/ ∑W_j
Normalisasi matriks X berdasarkan persamaan
sehingga diperoleh matriks ternormalisasi S.
wj adalah pangkat bernilai positif untuk atribut keuntungan, dan bernilai negatif untuk atribut biaya.
Lakukan perangkingan dengan menggunakan persamaan :
.

Menghitung metode Weighted product dengan PHP.
Data Matrix calo kepala unit sistem informasi :

Data Matrik Metode Weighted Product

Bobot (w) :

0.35

0.25

0.15

Tahap melakukan perhitungan metode WP dengan PHP :

Lakukan perbaikan bobot :

$bobot = array(0.35, 0.25, 0.25, 0.15);

$jumBobot = array_sum($bobot);

echo "<h3>Bobot Awal</h3>";

echo "<table
 border=1 style='border-collapse:collapse; border:solid 1px #000' 
width=300><tr><td>Bobot (w)</td>";

for($i=0; $i<4; $i++)

    echo "<td>$bobot[$i]</td>";

echo "</tr></table>";   

//Perbaikan bobot

//Simpan di array newBobot

$newBobot = array();

echo "<h3>Bobot Baru</h3>";

echo "<table
 border=1 style='border-collapse:collapse; border:solid 1px #000' 
width=300><tr><td>Bobot (W new)</td>";

for($i=0; $i<4; $i++){

    $newBobot[$i] = $bobot[$i] / $jumBobot;

    echo "<td>$newBobot[$i]</td>";

}

echo "</tr></table>";

Normalisasi Matrix

//Lakukan Normalisasi dengan rumus pada langkah 2

//Hitung Normalisasi tiap Elemen

$sql2 = mysql_query("SELECT * FROM tbmatrik");

//Buat tabel untuk menampilkan hasil

echo "<H3>Matrik Normalisasi</H3>

<table width=300 style='border:1px; #ddd; solid; border-collapse:collapse' border=1>

    <tr>

        <td>No</td><td>Nama</td><td>Nilai S</td>

    </tr>

";

$no = 1;

$i = 0;

//Buat variabel S array

$normS = array();

while ($dt2 = mysql_fetch_array($sql2)) {

//Hitung S per baris

    $normS[$i] = pow($dt2['Kriteria1'], $newBobot[0]) * pow($dt2['Kriteria2'], $newBobot[1]) * pow($dt2['Kriteria3'], $newBobot[2]) * pow($dt2['Kriteria4'], $newBobot[3]);

    echo "<tr>

        <td>$no</td><td>".getNama($dt2['idCalon'])."</td><td>".round($normS[$i],2)."</td>

    </tr>";

$no++;

$i++;

}

echo "</table>";

Lakukan Perangkingan

//Proses perangkingan dengan rumus langkah 3

//Jumlahkan Terlebih dahulu nilai S

$jums = round(array_sum($normS),2);

$sql3 = mysql_query("SELECT * FROM tbmatrik");

//Buat tabel untuk menampilkan hasil

echo "<H3>Perangkingan</H3>

Nilai Sum S = $jums

<table width=300 style='border:1px; #ddd; solid; border-collapse:collapse' border=1>

    <tr>

        <td>No</td><td>Nama</td><td>Rangking</td>

    </tr>

";

$no = 1;

$i=0;

//Kita gunakan rumus (s/ sum(s))

while ($dt3 = mysql_fetch_array($sql3)) {

    echo "<tr>

        <td>$no</td><td>".getNama($dt3['idCalon'])."</td>

        <td>"

        .round($normS[$i]/ $jums,2)."</td>

    </tr>";

$no++;

$i++;

}

echo "</table>";

Berikut adalah hasil dari source code sistem pendukung keputusan Weighted Product :

Hasil SPK Metode WP

Minggu, 09 Maret 2014

SPK Menggunakan Metode SAW

SAW adalah Simple Additive Weighting. Dalam hal pengambilan keputusan, metode SAW cukup populer. SAW merupakan metode penjumlahan terbobot suatu alternatif dari beberapa atribut (kriteria) yang didalamnya terdapat proses normalisasi dengan hasil akhir urutan alternatif yang paling disarankan berdasar algoritma metode tersebut.
Ada beberapa langkah untuk mengerjakan pemecahan pengambilan keputusan dari suatu set alternatif dengan beberapa kriteria menggunakan metode SAW. Sesuai dengan algoritma yang ada dari berbagai sumber, sebagai berikut:
1. Menentukan nilai kriteria Cj pada suatu set alternatif Ai. Beserta bobot preferensi (Wj) setiap kriteria Cj
2. Menghitung Rij dengan formula normalisasi sehingga mendapat matrik ternormaisasi.
Rij = Cij / Max(Cij) → jika j adalah atribut / kriteria benefit (untung = nilai lebih besar lebih dipilih)
Rij = Min(Cij) / Cij → jika j adalah atribut / kriteria cost (biaya = nilai lebih kecili lebih dipilih)
3. Menghitung nilai preferensi Vi, lalu mengurutkan dari yang terbesar.

Vi merupakan hasil akhir metode SAW, dengan nilai yang terbesar merupakan alternatif yang disarankan
Wj merupakan bobot preferensi untuk setiap kriteria Cj
Rij merupakan hasil normalisasi
Berikut script dari perhitungan tersebut:
Contoh kasus:
Terdapat 3 alternatif dan 5 kriteria sebagai berikut:
Dengan bobot preferensi: PPKN (30), IPA (25), IPS (20), SENI (10), KOMPUTER (15)

script:
<?php
//variabel jml alternatif
$jml = 3;
//variabel nama alternatif (sesuai urutan soal)
$a = array(‘ANDI’,'BOBI’,'CIAN’);
//variabel jml kriteria
$jk = 5;
//variabel nama kriteria
$k = array(‘PPKN’,'IPA’,'IPS’,'SENI’,'KOMPUTER’);
//variabel bobot kriteria (sesuai urutas soal: PPKN – IPA – IPS – SENI – KOMPUTER)
$w = array(’30′,’25′,’20′,’10′,’15′);
//variabel skor kriteria (sesuia urutan nama pd soal: ANDI – BOBI – CIAN )
$k1 = array(’80′,’70′,’60′); //PPKN
$k2 = array(’64′,’75′,’90′); //IPA
$k3 = array(’78′,’90′,’86′); //IPS
$k4 = array(’89′,’67′,’65′); //SENI
$k5 = array(’85′,’90′,’70′); //KOMPUTER
//pemasangan alternatif terhadap kriteria
$j=1;
for ($i=0; $i < $jml; $i++) {

$alt[$j][1] = $k1[$i]; //kriteria1 utk alternatif ke-i
$alt[$j][2] = $k2[$i]; //kriteria2 utk alternatif ke-i
$alt[$j][3] = $k3[$i]; //kriteria3 utk alternatif ke-i
$alt[$j][4] = $k4[$i]; //kriteria3 utk alternatif ke-i
$alt[$j][5] = $k5[$i]; //kriteria3 utk alternatif ke-i
$alt[$j][6] = $a[$i]; //nama alternatif ke-i
$j++;

}
//Contoh untuk program ini SEMUA Kriteria berkaidah MAX ,,
//untuk kaidah MIN/MAX sesuaikan rumus, diprogram PERLU menambahkan kode kondisi kriteria sesuai kaidah
//Mencari Max pada setiap set nilai kriteria dari semua alternatif.
//Contoh pada set kriteria PPKN nilai max adl 80.
$max[0] = max($k1); //PPKN
$max[1] = max($k2); //IPA
$max[2] = max($k3); //IPS
$max[3] = max($k4); //SENI
$max[4] = max($k5); //KOMPUTER
echo ‘<br><fieldset><legend><h2>Perhitungan SAW</h2></legend>’;
echo ‘<h3>Hasil Perhitungan</h3>’;
echo ‘Tabel Bobot Kriteria SAW’;
echo ‘<table border=1 bordercolor=silver cellspacing=0 cellpadding=5>
<tr bgcolor=#779999>’;

for ($i=0; $i < $jk; $i++){

echo “<th>$k[$i]</th>”;

}

echo “</tr><tr>”;
for ($i=0; $i < $jk; $i++){

echo “<td>$w[$i]</td>”;

}

echo “</tr></table></br>”;
echo ‘Tabel Hitungan Normalisasi SAW’;
echo ‘<table border=1 bordercolor=silver cellspacing=0 cellpadding=5>
<tr bgcolor=#779999><th>No</th><th>Nama</th>’;
for ($i=0; $i < $jk; $i++){

echo “<th>$k[$i]</th>”;

}

echo ‘</tr><tr>’;

//tahap normalisasi
//dari alternatif 1 s.d 3

for ($i=1; $i <= $jml; $i++){
echo “<td>$i</td><td>”.$alt[$i][6].”</td>”;
//$V[$i] = 0;

// dari kriteria 1 s.d 5

for ($k=1; $k <= $jk; $k++){
$R[$i][$k] = $alt[$i][$k]/$max[$k-1]; //formula untuk kaidah MAX
echo “<td>”.round($R[$i][$k],5).”</td>”; //hasil pembulatan 5 angka dibelakan koma
}
echo ‘</tr>’;
}
echo ‘</table><br>’;
//tahap hitung V
for ($i=1; $i <= $jml; $i++){ //loop sebanyak alternatif
$V = 0;
for ($k=1; $k <= $jk; $k++){ //loop sebanyak kriteria
$V = $V + $R[$i][$k]*$w[$k-1]; //hasil Vi, didapat dari jumlah perkalian antara Wj dengan Rij
//echo $V.’<br>’;
}
$Vi[$i] = $V; //simpan hasil V dlm array sesuai alternatif
}
for ($i=1; $i <= $jml; $i++){
$nama[$i] = $alt[$i][6]; //menyimpan varibel nama alternatif ke single array
}
echo ‘Tabel Urutan Akhir SAW’;
echo ‘<table border=1 bordercolor=silver cellspacing=0 cellpadding=5>
<tr bgcolor=#779999><th>No</th><th>Nama</th><th>Nilai V</th></tr>’;

//tahap pengurutan hasil

$jvi = array_combine($nama, $Vi); //menggabungkan array nama dg array Vi
//print_r($jvi);
arsort($jvi); //mengurutkan berdasarkan Vi terbesar
$n = 0;
foreach ($jvi as $x => $val){ //untuk setiap $x = nama dan $val = Vi
$n = $n+1; $vsaw=round($val,5);
echo ‘<tr>’;
echo “<td>$n</td><td>”.$x.”</td>”;
echo “<td>”.$vsaw.”</td>”;
echo ‘</tr>’;
}
echo ‘</table><br></fieldset>’;
?>